As we know, the process can allocate & deallocate memory using malloc & free in C language. But do you ever consider what happens behind the scene ? or How do malloc & free work? Let see
Contents
Allocating Memory on the Heap
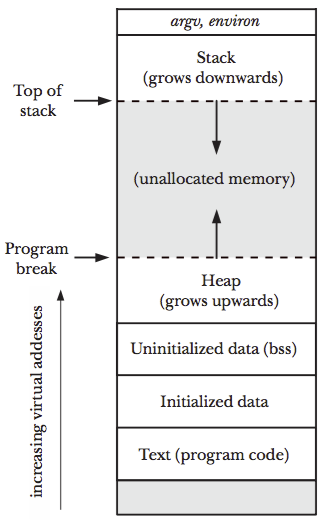
- A process can allocate memory by increasing the size of the heap.
- Heap is a variable-size segment of contiguous virtual memory that begins just after the uninitialized data segment of a process and grows & shrinks as memory allocated and freed.
- The current limit of the heap referred to as the program break which is just at the end of the uninitialized data segment in process address space.
- Resizing the heap (i.e., allocating or de-allocating memory) is as simple as telling the kernel to adjust its idea of where the process’s program break is.
- To allocate memory, C programs normally use the malloc family of functions, which we describe shortly. However, we begin with a description of
brk()&sbrk(), upon which the malloc functions are based.
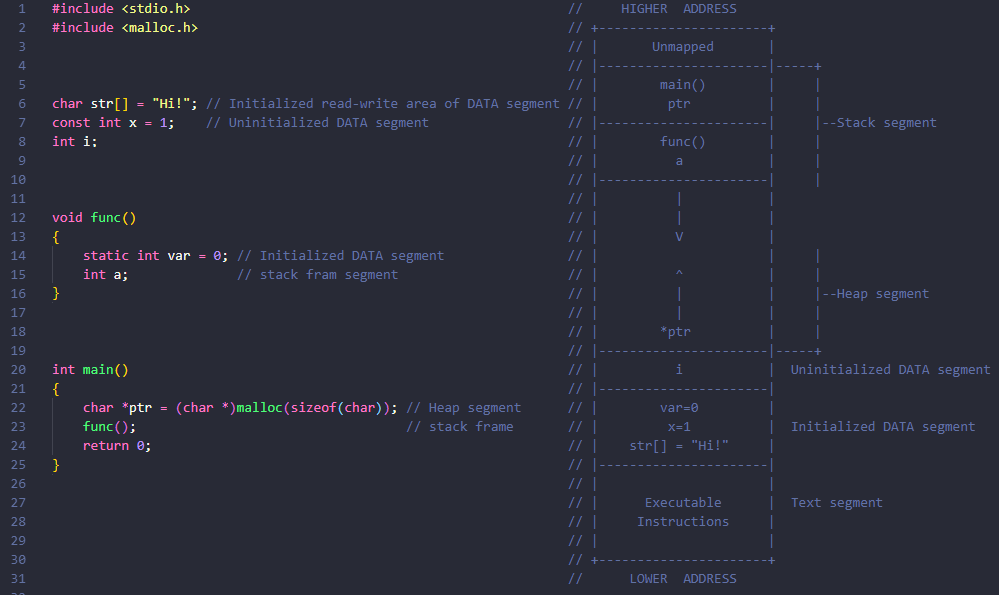
- Pre-requisites: Memory layout of C program OR Understanding of process address space
brk() & sbrk()
#include <unistd.h> int brk(void end_data_segment); void *sbrk(intptr_t increment);
- The
brk()is a system call which sets the program break to the location specified byend_data_segment. Since virtual memory is located in units of pages,end_data_segmentis effectively rounded up to the next page boundary. - A call to
sbrk()adjusts the program break by adding an increment to it. On Linux,sbrk()is a library function implemented on top ofbrk(). On success,sbrk()returns the previous address of the program break. In other words, if we have increased the program break, then the return value is a pointer to the start of the newly allocated block of memory. The callsbrk(0)returns the current setting of the program break without changing it. This can be useful if we want to track the size of the heap, perhaps to monitor the behaviour of a memory allocation package. - After the program break increased, the program may access any address in the newly allocated area, but no physical memory pages allocated yet. The kernel automatically allocates new physical pages on the first attempt by the process to access addresses in those pages.
How Does malloc & free Work?
malloc
- When you malloc a block, it first checks how much memory you requested.
- There are 2 ways to get memory from the system: 1.
mmap(), 2.brk(). - When you request some byte to be allocated by malloc it checks for
MMAP_THRESHOLDlimit(this also depends upon library implementations). If you request more than that limit, thenmmap()system call used to obtain the requested memory. - Else it uses
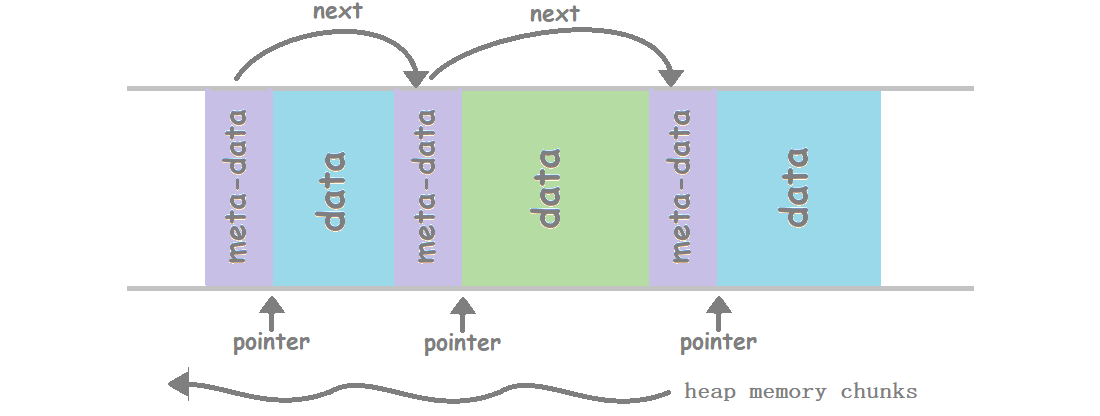
brk()syscall, increments the program break size & gives you a pointer to start of newly allocate contiguous block. - Whichever procedure it follows, it allocates a bit more memory than you asked for. This extra memory(also known as meta-data) used to store information such as the size of the allocated block. And a link to the next free/used a block in a chain of blocks, and sometimes some guard data(that helps the system to detect if you write past the end of your allocated block).
- Also, most allocators will round-up the total size and/or the start of your part of the memory to a multiple of bytes (e.g. on a 64-bit system may align the data to a multiple of 64 bits (8 bytes) as accessing data from non-aligned addresses can be more difficult and inefficient for the processor/bus), so you may also end up with some “padding” (unused bytes).
free
- As we know so far that we allocate the memory just by increasing the program’s break.
- And upon your intellect, you must be thinking that free will lower this program break.
- But it’s not, free simply adds the block of memory to list of free blocks that are recycled by future calls to
malloc(). But why? - Well, the block of memory being freed is typically somewhere in the middle of the heap, rather than at the end, so that lowering the program break is not possible.
Will malloc Allocates Contiguously in Memory or It Scattered?
- Yes & no both, Here is why!
- In a typical OS, there exists the concepts of virtual memory and physical memory.
- Each process has its virtual memory range which is contiguous.
- When you allocate memory through malloc, the program break increased with respect to virtual memory. So your allocated byte is contiguous.
- But the OS, behind the scenes, is busy mapping virtual memory allocations onto real blocks of physical memory which do not be contiguous because this is how VMM(Virtual Memory Manager) works. You can read more about it here.
How Does free Know How Much to Free?
- If you still can not figure out the answer to this question, you may read the above topics again.
- Anyway. When you call
malloc(), you specify the amount of memory to allocate. The amount of memory used is slightly more than this and includes extra information that records (at least) how big the block is. - You can’t (reliably) access that other information – and nor should you.
- When you call
free(), it simply looks at the extra information to find out how big the block is.
Do you like it☝️? Get such articles directly into the inbox…!?